Trees [structures that generate one bit of the result]¶
Setup (RUN ME before executing any code in this section)¶
[1]:
!pip install --upgrade git+https://github.com/tdene/synth_opt_adders.git
Defaulting to user installation because normal site-packages is not writeable
Collecting git+https://github.com/tdene/synth_opt_adders.git
Cloning https://github.com/tdene/synth_opt_adders.git to /tmp/pip-req-build-a8rtu625
Running command git clone --filter=blob:none --quiet https://github.com/tdene/synth_opt_adders.git /tmp/pip-req-build-a8rtu625
Resolved https://github.com/tdene/synth_opt_adders.git to commit 8fd7d6c3257f73ae3e278281be636dc098a9b015
Preparing metadata (setup.py) ... done
Requirement already satisfied: Pillow in /home/tdene/.local/lib/python3.8/site-packages (from pptrees==1.0.8) (9.1.1)
Requirement already satisfied: graphviz in /home/tdene/.local/lib/python3.8/site-packages (from pptrees==1.0.8) (0.19.1)
Requirement already satisfied: networkx in /home/tdene/.local/lib/python3.8/site-packages (from pptrees==1.0.8) (2.7)
Requirement already satisfied: pydot in /home/tdene/.local/lib/python3.8/site-packages (from pptrees==1.0.8) (1.4.2)
Requirement already satisfied: pyparsing>=2.1.4 in /home/tdene/.local/lib/python3.8/site-packages (from pydot->pptrees==1.0.8) (3.0.7)
WARNING: You are using pip version 22.0.4; however, version 22.1.2 is available.
You should consider upgrading via the '/usr/bin/python3 -m pip install --upgrade pip' command.
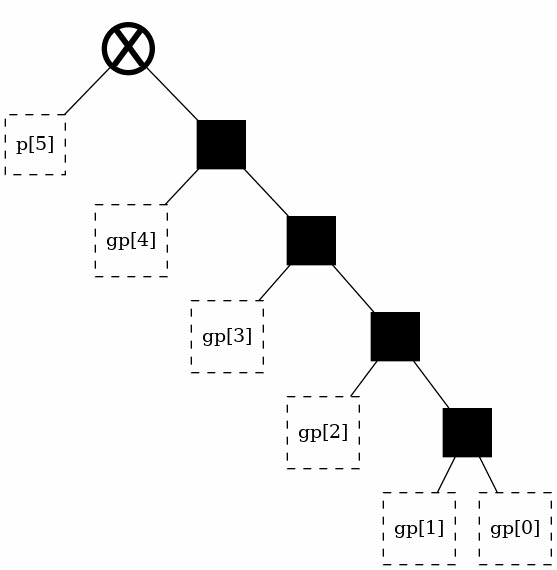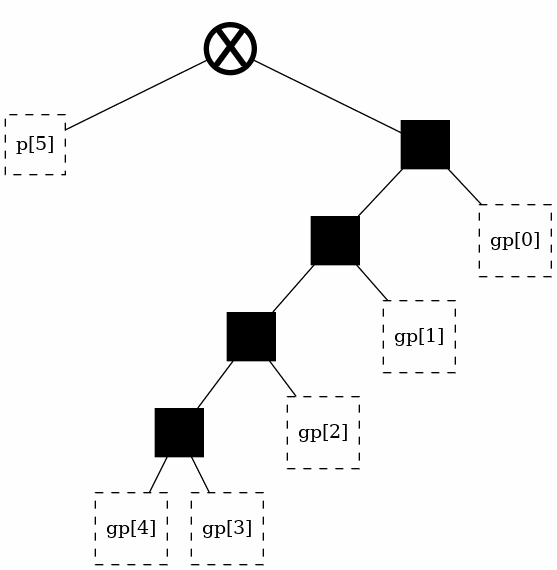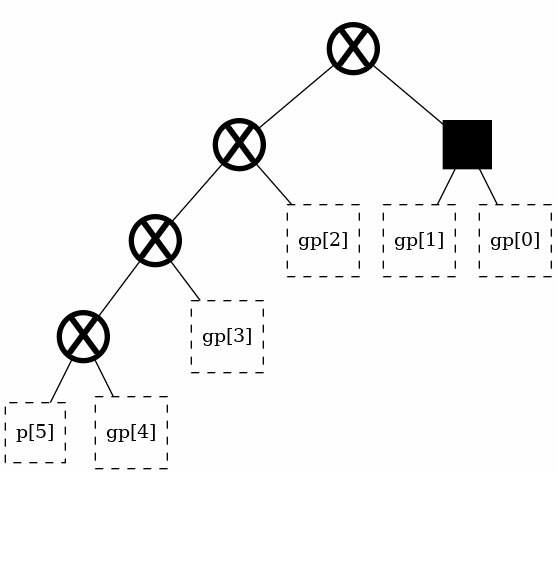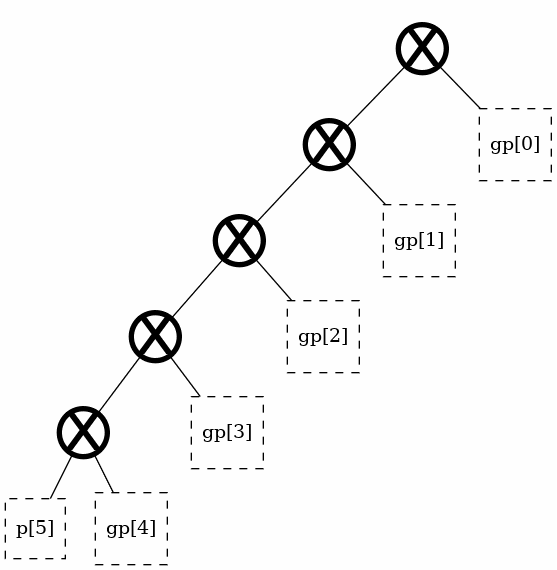
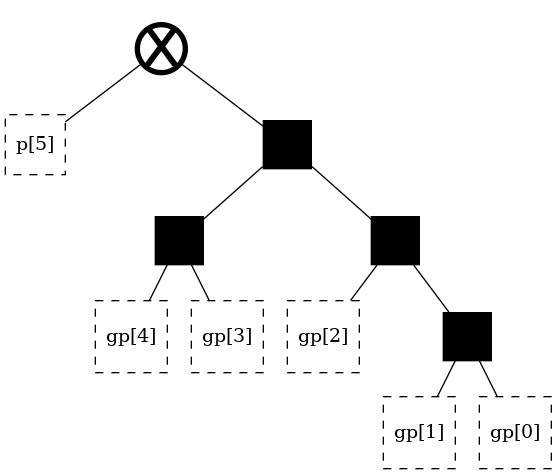
Generating a classic structure [LEGACY]¶
Note: this section is shown simply for illustrative purposes. Many of the functions used here-in are legacy functions, supported only for backwards compatibility with past diagrams and methods. The code in this section should be avoided in production.
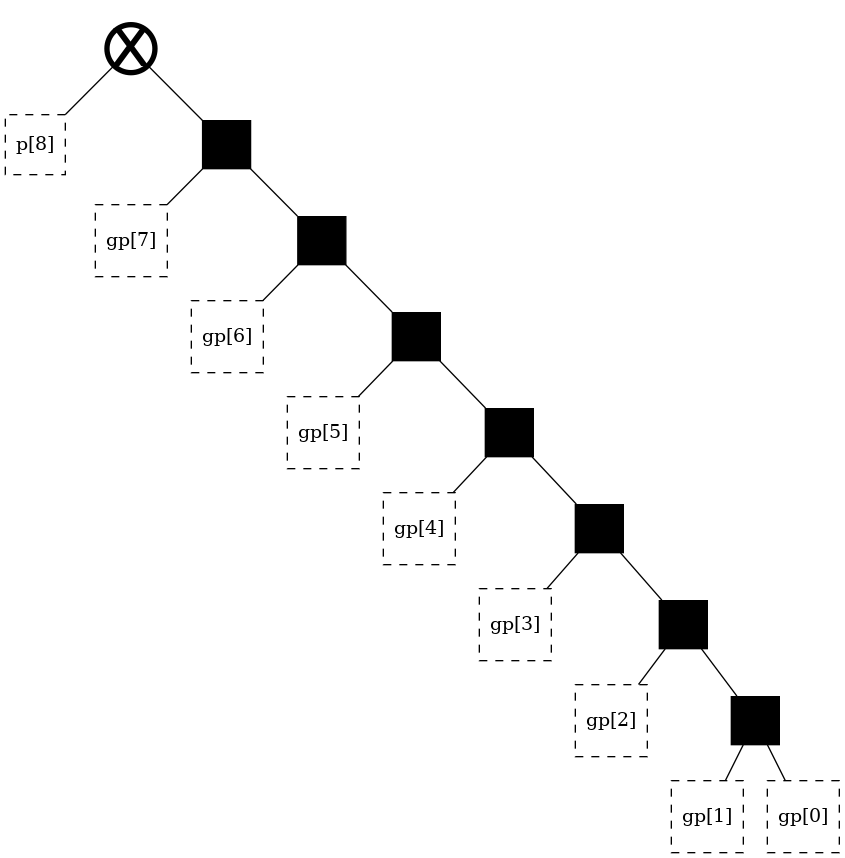
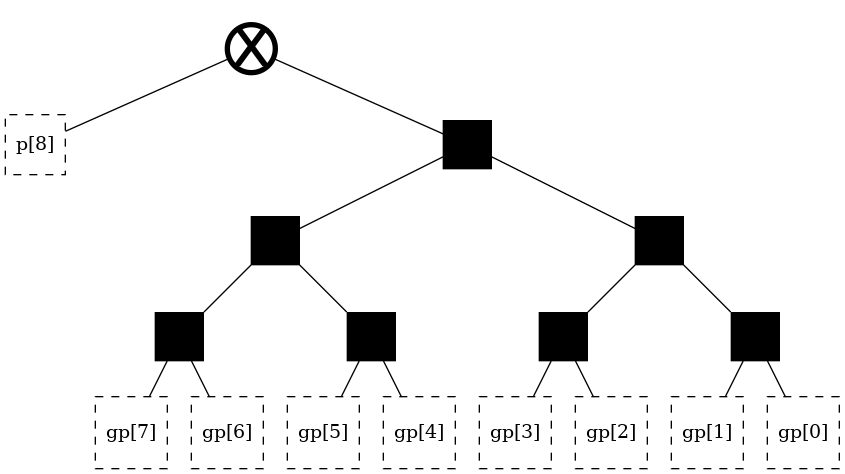
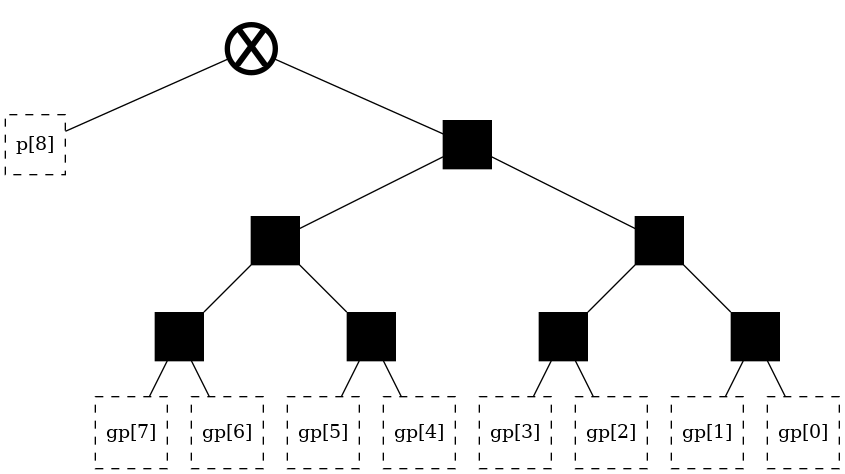
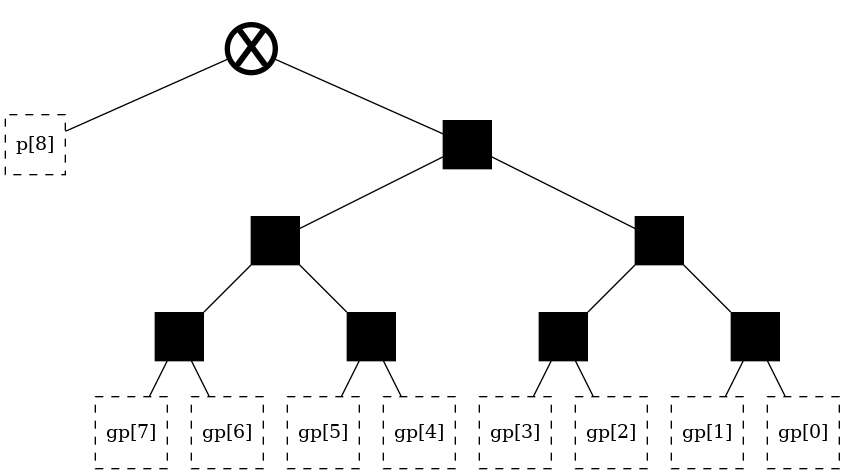
The theory section discusses four classic, regular, structures. These architectures can be readily generated under this library using aliases. Note again that the “alias” parameter is legacy, supported only for backwards compatibility, and should not actually be used.
[4]:
from pptrees.AdderTree import AdderTree as tree
width = 9
t = tree(width, alias = "ripple-carry")
t
[4]:
[5]:
from pptrees.AdderTree import AdderTree as tree
width = 9
t = tree(width, alias = "sklansky")
t
[5]:
[6]:
from pptrees.AdderTree import AdderTree as tree
width = 9
t = tree(width, alias = "kogge-stone")
t
[6]:
[7]:
from pptrees.AdderTree import AdderTree as tree
width = 9
t = tree(width, alias = "brent-kung")
t
[7]:
How many possible trees are there?¶
[8]:
from pptrees.util import catalan
width = 9
print("There are {0} possible trees of width {1}".format(catalan(width-1),width))
There are 1430 possible trees of width 9
What do all of these trees look like?¶
Note that while generating the tree structures is fast, generating the diagrams can be very slow.
[2]:
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width = 6
# Generate all trees of width 9
list_of_trees=[]
for a in range(catalan(width-1)):
t = tree(width, start_point = a)
list_of_trees.append(t)
# Visualize the trees in GIF form
from pptrees.util import display_gif as display_gif
from IPython.display import Image
Image(display_gif(list_of_trees))
[2]:
How do I get the tree that I want?¶
The number of total possible trees is known. Thus it is possible to assign an integer ID to every possible structure. The labeling I chose is based on an order that arose naturally. If you, reader, happen to know the name of this specific tree traversal, please contact me as I’ve so far been unable to find it in literature.
To get a desired structure, simply initialize it with its label.
[ ]:
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width = 33
# First, check the total number of structures
print("There are {0} possible trees of width {1}".format(catalan(width-1),width))
print("Here is one of them:")
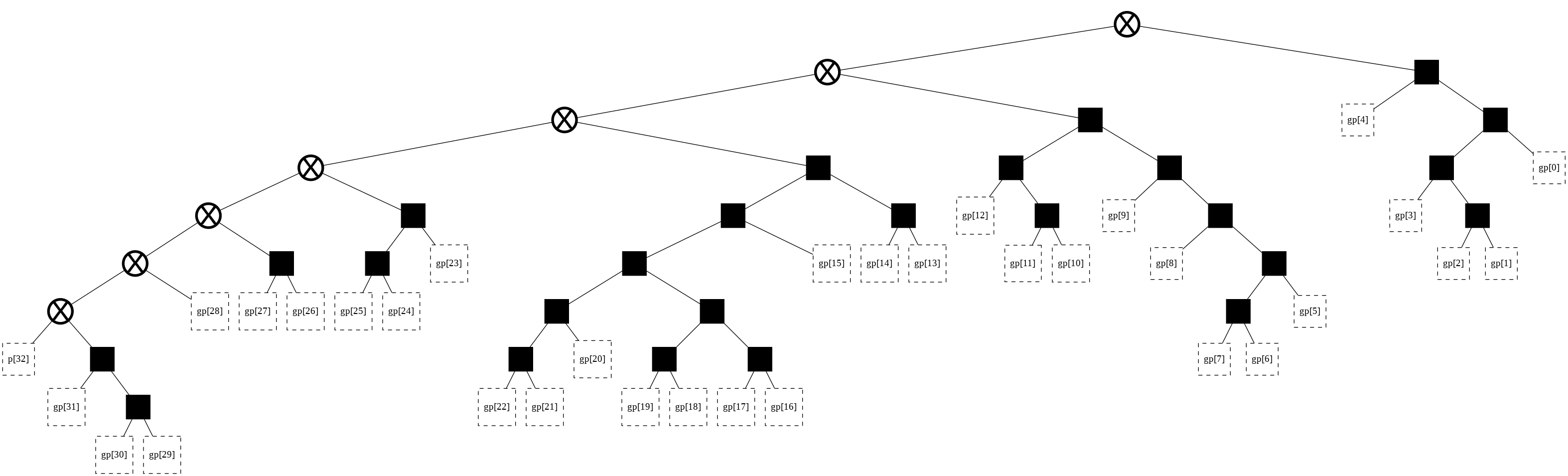
t = tree(width, start_point = 33416136136136512)
t
There are 55534064877048198 possible trees of width 33
Here is one of them:
[ ]:
print("Here is another one:")
t = tree(width, start_point = catalan(width-2)//2)
t
Here is another one:
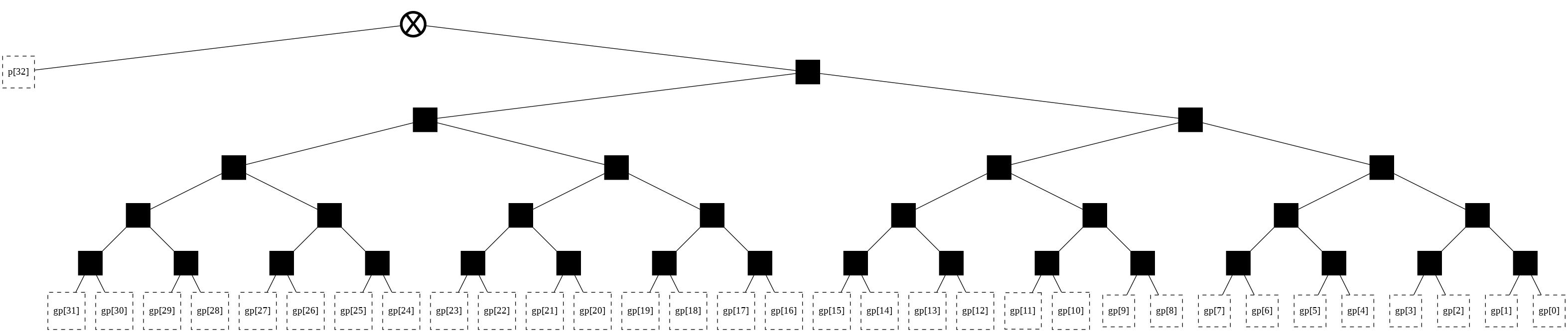
This order begins and ends with slower, O(n), structures. In the middle are better-balanced, O(lg n). However, each of these possible structures has useful delay, power, or area characteristics when viewed as a part of the complete adder (forest) structure.
Okay, I have a tree. How do I make it faster?¶
Theory
In general, for the tree to be faster, it must be more balanced. Keep in mind, however, that the speed of each individual tree is greatly affected by the forest it is a part of.
If every tree in a forest is left-balanced (more commonly known as “complete”), theoretically each of the individual trees will be very fast, but as part of the greater forest they will each incur a delay penalty due to a large amount of necessary routing tracks.
If each tree in a forest is right-balanced, theoretically each of the individual trees will be very fast, but as part of the greater forest they will each incur a delay penalty due to a large amount of fan-out.
Application
The library supports four methods of transforming trees.
left_rotate - Rotates a given node left
right_rotate - Rotates a given node right
left_shift - Shifts a given node left into another subtree; the equivalent of AVL trees’ RL rotate, except this is a generalized RRRRRRRR…L rotate.
right_shift - Shifts a given node right into another subtree; the equivalent of AVL trees’ LR rotate, except this is a generalized LLLLLLLL…R rotate.
[ ]:
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width = 10
# First, check the total number of structures
print("There are {0} possible trees of width {1}".format(catalan(width-1),width))
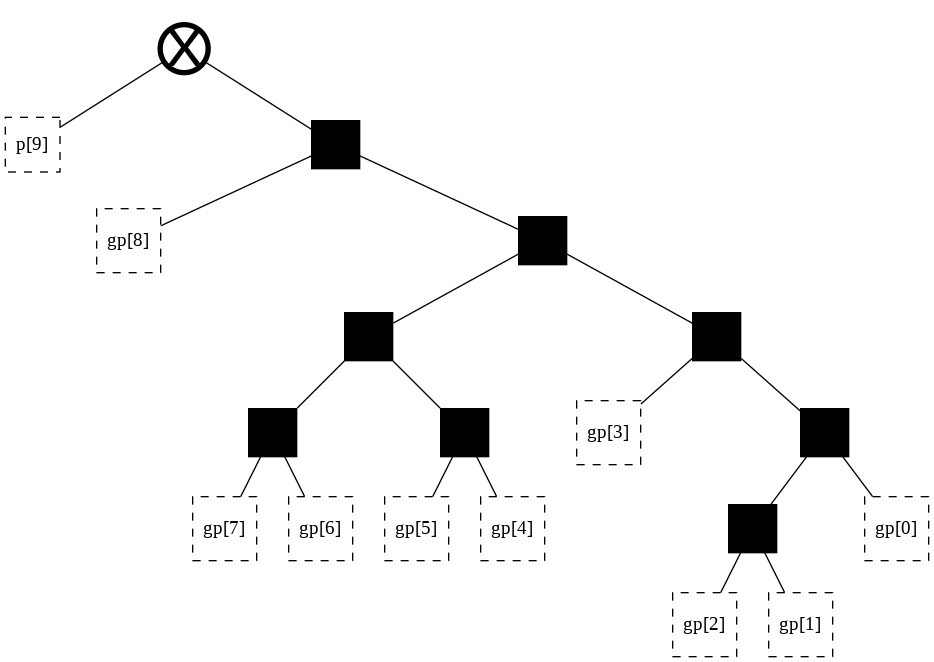
# Start at some initial point
t = tree(width, start_point = 209)
t
There are 4862 possible trees of width 10
[ ]:
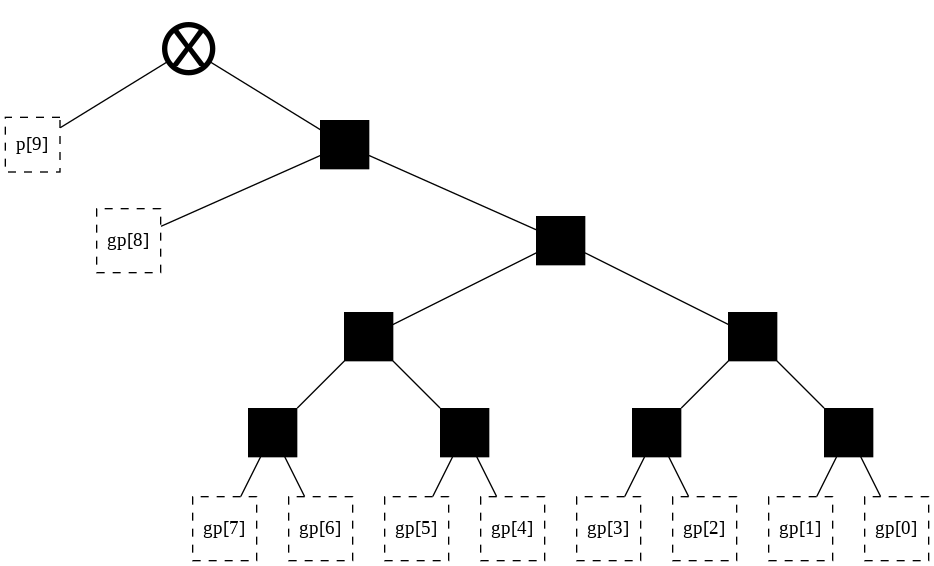
# Speed up the tree
t = tree(width, start_point = 209)
t.right_rotate(t.root[1][1][1][1][0])
t.left_rotate(t.root[1][1][1][1])
t
[ ]:
# Or do it with a left-shift (RL rotate)
t = tree(width, start_point = 209)
t.left_shift(t.root[1][1][1][1][0])
t
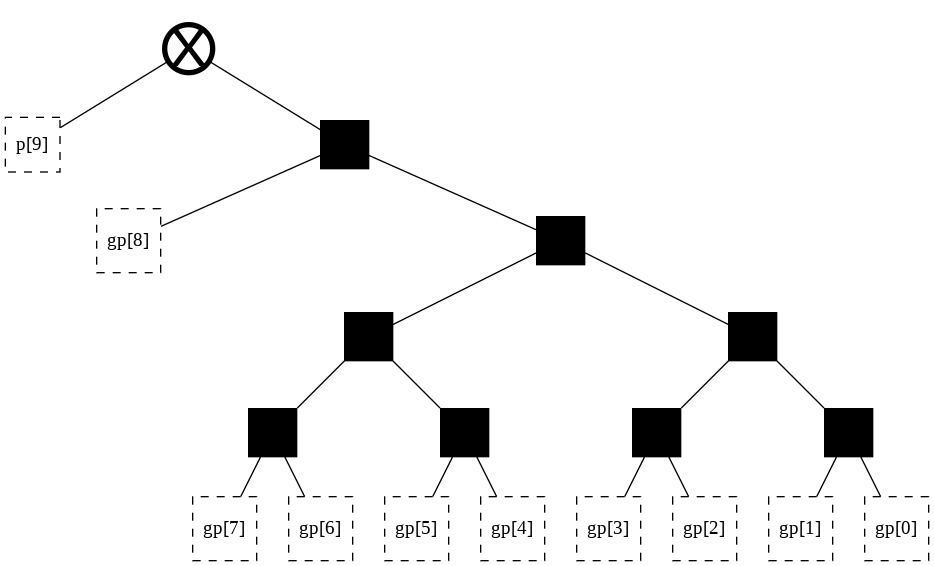
[ ]:
# Balance the tree even more by using sparseness
t = tree(width, start_point = 209)
t.left_shift(t.root[1][1][1][1][0])
t.left_shift(t.root[1])
t
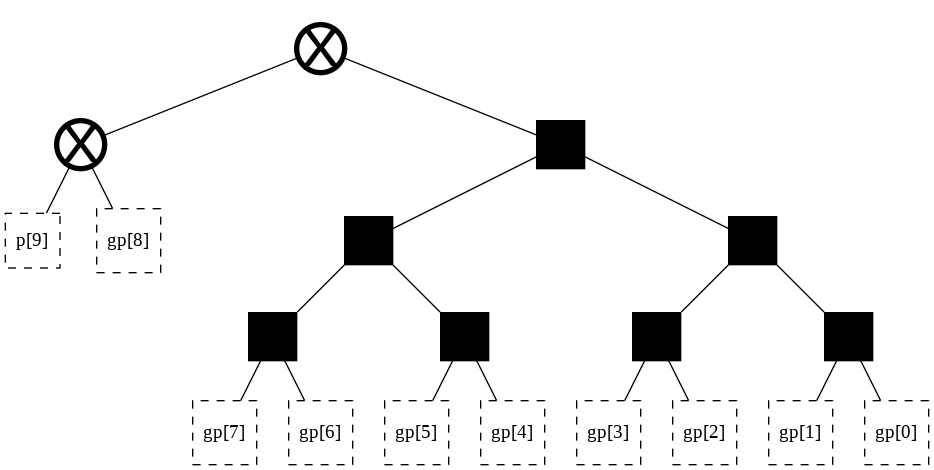
Okay, now how do I make a tree more power-efficient? Or smaller?¶
Theory
Both area and power consumption are determined primarily not by an individual tree, but rather by the forest it is a part of.
Both area and power consumption fall with an increasing number of shared nodes between trees. That is why serial adders have smaller area than parallel ones, and why the Brent-Kung structure has smaller area than the Kogge-Stone one.
In general, the further right-balanced a tree is, the more nodes it is able to share. This is however just a rule of thumb.
Application
See the following example.
[4]:
# Let's say we only want the 6th and 7th bit of a sum.
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width_big = 7
width_small = 6
# First, check the total number of structures
print("There are {0} possible trees of width {1}".format(catalan(width_big-1),width_big))
print("There are {0} possible trees of width {1}".format(catalan(width_small-1),width_small))
# Next, initialize two random trees
t_big = tree(width_big, start_point = 72)
t_small = tree(width_small, start_point = 12)
There are 132 possible trees of width 7
There are 42 possible trees of width 6
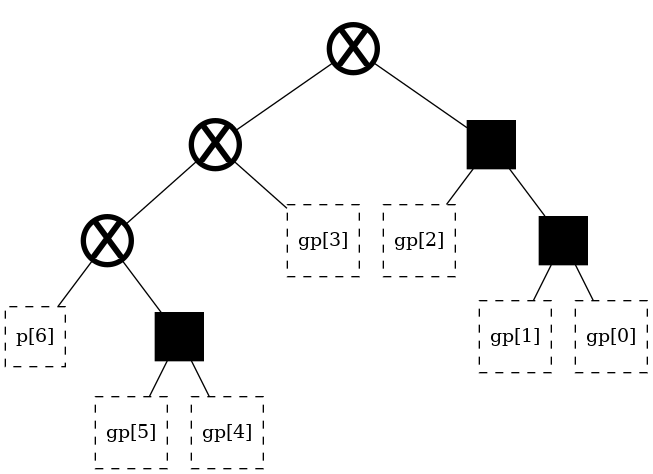
[5]:
t_big
[5]:
[6]:
t_small
[6]:
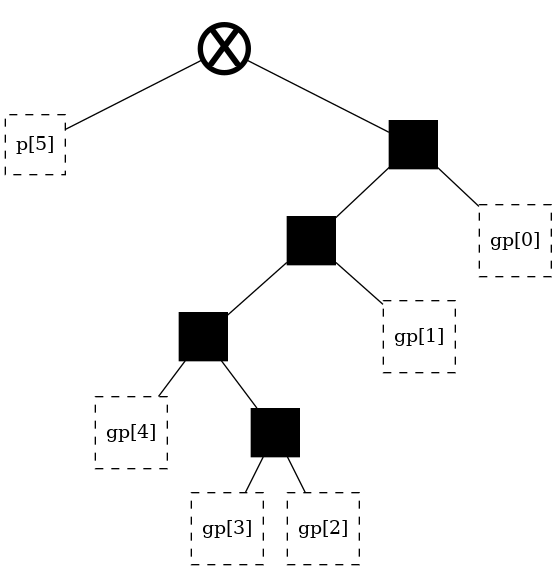
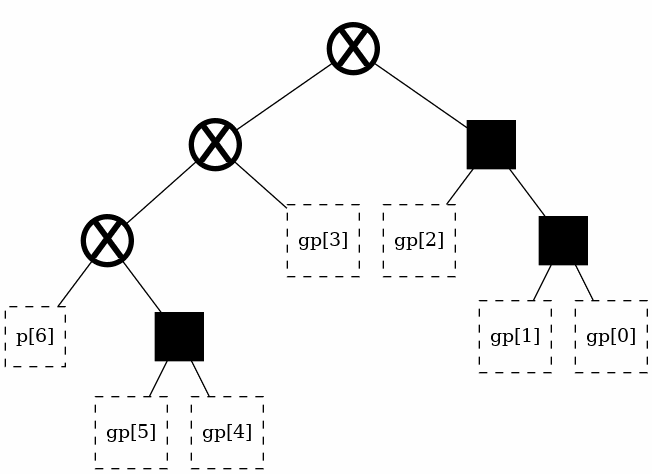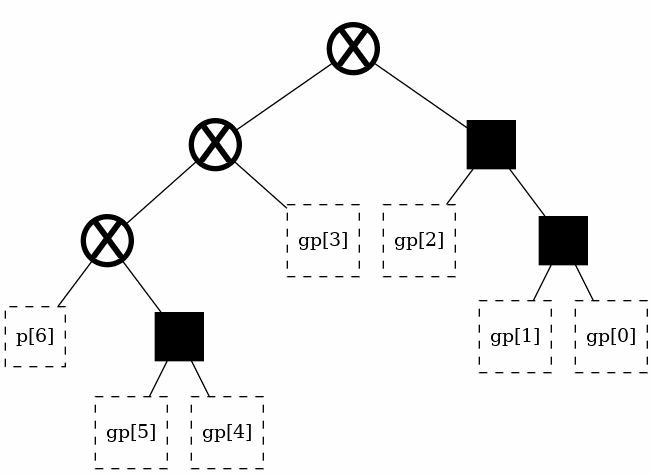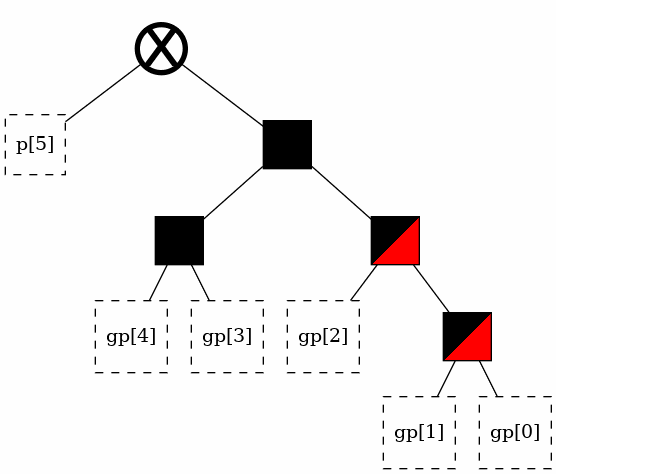
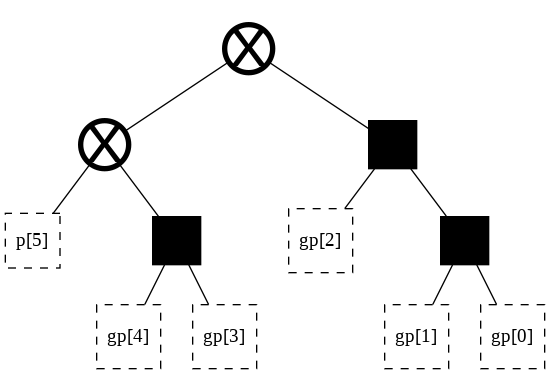
Note that these two trees have no nodes in common. Let’s give them some.
[7]:
t_small = tree(width_small, start_point = 12)
# Make the left-hand side of the trees similar
t_small.right_rotate(t_small.root[1][0])
t_small.right_shift(t_small.root[1][0][1])
t_small
[7]:
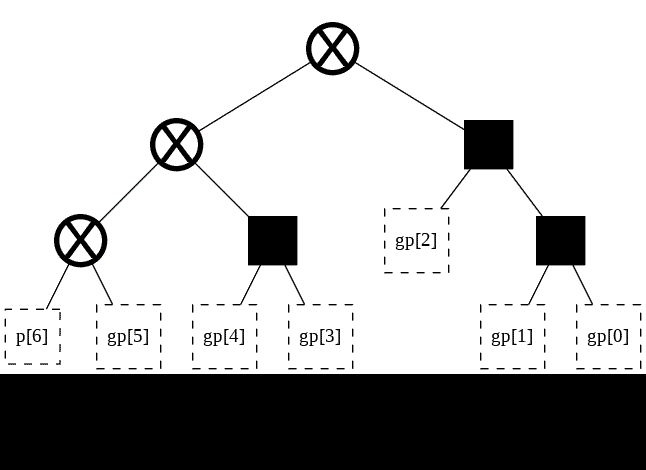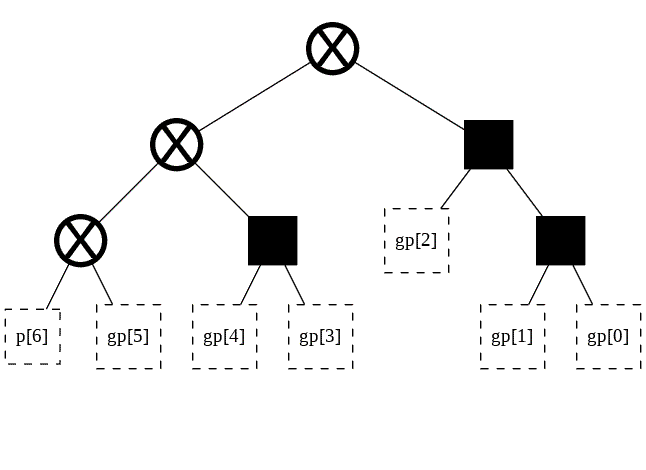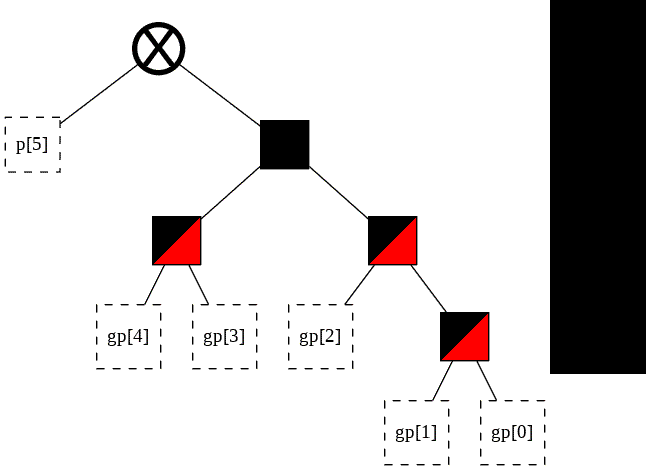
The two trees have gone from sharing 0 nodes, to sharing 2 nodes. Area and power consumption has been reduced.
We can visualize the shared nodes by creating a make-shift forest and using its methods.
The nodes that have been painted partially red in t_small are shared between the two trees. This is merely cosmetic, intended to serve as a visual indicator.
Note that the equivalent nodes in t_big have not been painted red. This is intentional. The red marks nodes that need not be implemented in hardware. Shared nodes only need to be implemented in hardware once, but they still need to be implemented that one single time.
[8]:
from pptrees.AdderForest import AdderForest as forest
f = forest(2, initialized_trees=[t_big, t_small])
f.reset_equivalent_nodes()
f.find_equivalent_nodes()
f
[8]:
[ ]:
f.reset_equivalent_nodes()
Let’s go even further
[ ]:
t_big = tree(width_big, start_point = 72)
# Make the right-hand side of the trees similar
t_big.right_shift(t_big.root[0][0][1])
t_big
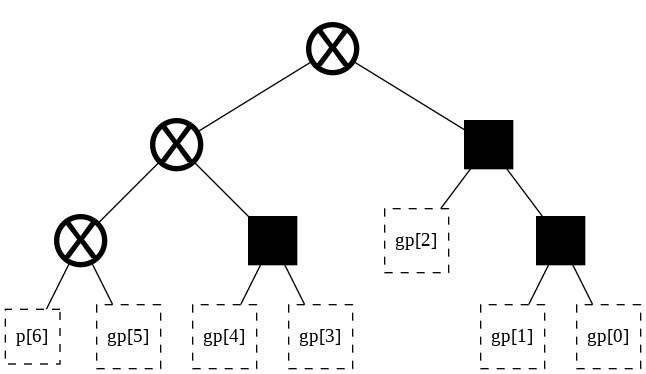
[ ]:
f = forest(2, initialized_trees=[t_big, t_small])
f.find_equivalent_nodes()
f
[ ]:
f.reset_equivalent_nodes()
The two trees now share 3 nodes. Also, t_big is now more balanced! Let’s make t_small a bit more balanced as well.
[ ]:
t_small = tree(width_small, start_point = 12)
# Make the left-hand side of the trees similar
t_small.right_rotate(t_small.root[1][0])
t_small.right_shift(t_small.root[1][0][1])
# Reduce the height of t_small
t_small.left_rotate(t_small.root[1])
t_small
[ ]:
f = forest(2, initialized_trees=[t_big, t_small])
f.find_equivalent_nodes()
f
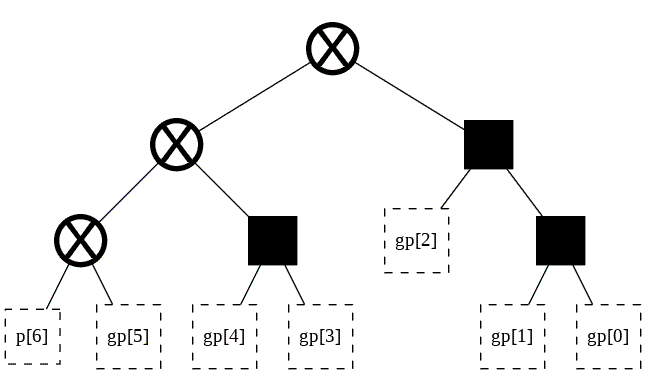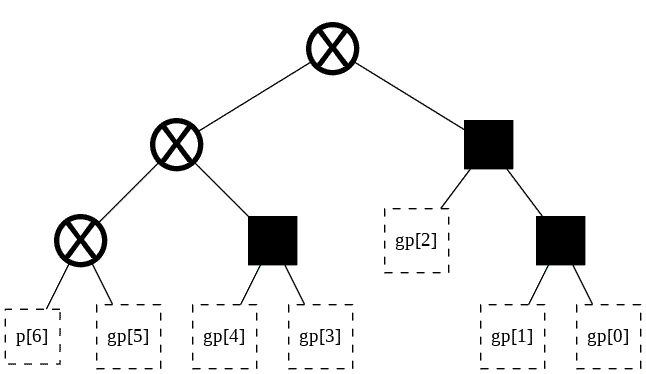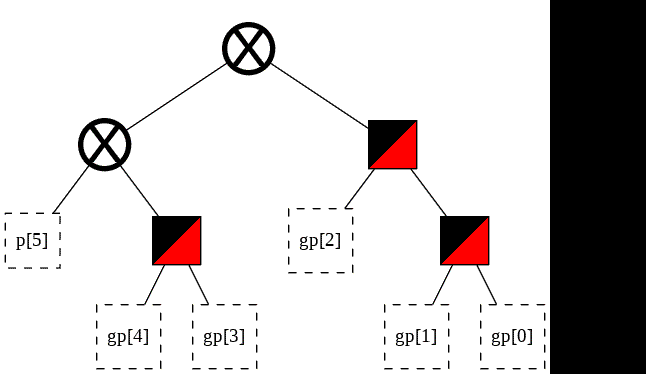
The two trees share 3 nodes still. The only way they could share more would be by making both of them serial.
Moreover, the two trees are both balanced, with O(lg n) delay.
This appears to be a good structure.
How do I get the ID of a tree after I’ve modified it?¶
The “rank” method gets the ID of a tree, while the “unrank” method creates a tree given a certain ID
[ ]:
# Let's say we only want the 6th and 7th bit of a sum.
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width_big = 7
width_small = 6
# First, check the total number of structures
print("There are {0} possible trees of width {1}".format(catalan(width_big-1),width_big))
print("There are {0} possible trees of width {1}".format(catalan(width_small-1),width_small))
# Next, initialize two random trees
t_big = tree(width_big, start_point = 72)
t_small = tree(width_small, start_point = 12)
# Make the right-hand side of the trees similar
t_big.right_shift(t_big.root[0][0][1])
# Make the left-hand side of the trees similar
t_small.right_rotate(t_small.root[1][0])
t_small.right_shift(t_small.root[1][0][1])
# Reduce the height of t_small
t_small.left_rotate(t_small.root[1])
print("The rank (ID) of the big tree is {0}".format(t_big.rank()))
print("The rank (ID) of the small tree is {0}".format(t_small.rank()))
There are 132 possible trees of width 7
There are 42 possible trees of width 6
The rank (ID) of the big tree is 70
The rank (ID) of the small tree is 19
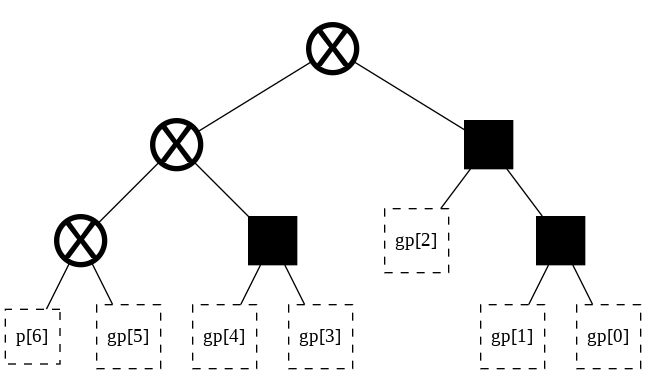
[ ]:
t = tree(width_big, start_point = 70)
t
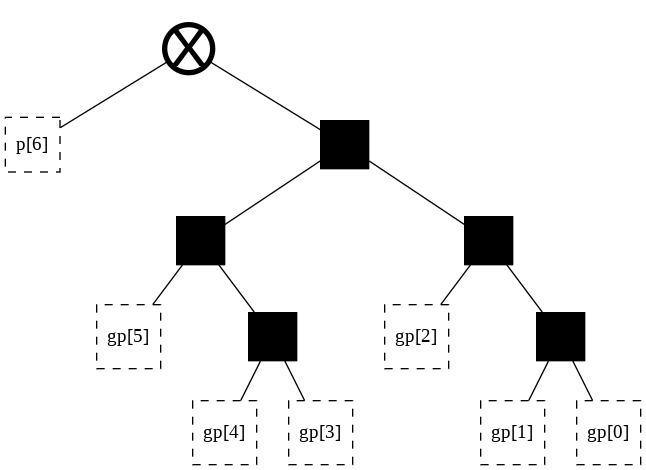
[ ]:
t = tree(width_big, start_point = 19)
t
Obtaining a PNG diagram¶
[ ]:
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width = 33
t = tree(width, start_point = 33416136136136512)
t.png("test.png")
Obtaining an HDL description¶
[9]:
from pptrees.AdderTree import AdderTree as tree
from pptrees.util import catalan
width = 33
t = tree(width, start_point = 33416136136136512)
_ = t.hdl("test.v")
[ ]:
!cat test.v
module adder(
input [32:0] a_in,
input [32:0] b_in,
output sum
);
// start of unnamed graph
wire n0, n1_adder, n2_adder, n3_adder, n4_adder, n5_adder, n6_adder, n7_adder, n8_adder, n9_adder, n10_adder, n11_adder, n12_adder, n13_adder, n14_adder, n15_adder, n16_adder, n17_adder, n18_adder, n19_adder, n20_adder, n21_adder, n22_adder, n23_adder, n24_adder, n25_adder, n26_adder, n27_adder, n28_adder, n29_adder, n30_adder, n31_adder, n32_adder, n33_adder, n34_adder, n35_adder, n36_adder, n37_adder, n38_adder, n39_adder, n40_adder, n41_adder, n42_adder, n43_adder, n44_adder, n45_adder, n46_adder, n47_adder, n48_adder, n49_adder, n50_adder, n51_adder, n52_adder, n53_adder, n54_adder, n55_adder, n56_adder, n57_adder, n58_adder, n59_adder, n60_adder, n61_adder, n62_adder, n63_adder, n64_adder, n65_adder, n66_adder, n67_adder, n68_adder, n69_adder, n70_adder, n71_adder, n72_adder, n73_adder, n74_adder, n75_adder, n76_adder, n77_adder, n78_adder, n79_adder, n80_adder, n81_adder, n82_adder, n83_adder, n84_adder, n85_adder, n86_adder, n87_adder, n88_adder, n89_adder, n90_adder, n91_adder, n92_adder, n93_adder, n94_adder, n95_adder, n96_adder, n97_adder, n98_adder, n99_adder, n100_adder, n101_adder, n102_adder, n103_adder, n104_adder, n105_adder, n106_adder, n107_adder, n108_adder, n109_adder, n110_adder, n111_adder, n112_adder, n113_adder, n114_adder, n115_adder, n116_adder, n117_adder, n118_adder, n119_adder, n120_adder, n121_adder, n122_adder, n123_adder, n124_adder, n125_adder, n126_adder, n127_adder;
assign sum = n111_adder ? n2_adder : n1_adder;
assign n127_adder = a_in[0]^b_in[0];
assign n126_adder = a_in[0]&b_in[0];
assign n125_adder = a_in[1]^b_in[1];
assign n124_adder = a_in[1]&b_in[1];
assign n123_adder = a_in[2]^b_in[2];
assign n122_adder = a_in[2]&b_in[2];
assign n119_adder = a_in[3]^b_in[3];
assign n118_adder = a_in[3]&b_in[3];
assign n113_adder = a_in[4]^b_in[4];
assign n112_adder = a_in[4]&b_in[4];
assign n110_adder = a_in[5]^b_in[5];
assign n109_adder = a_in[5]&b_in[5];
assign n108_adder = a_in[6]^b_in[6];
assign n107_adder = a_in[6]&b_in[6];
assign n106_adder = a_in[7]^b_in[7];
assign n105_adder = a_in[7]&b_in[7];
assign n100_adder = a_in[8]^b_in[8];
assign n99_adder = a_in[8]&b_in[8];
assign n96_adder = a_in[9]^b_in[9];
assign n95_adder = a_in[9]&b_in[9];
assign n92_adder = a_in[10]^b_in[10];
assign n91_adder = a_in[10]&b_in[10];
assign n90_adder = a_in[11]^b_in[11];
assign n89_adder = a_in[11]&b_in[11];
assign n86_adder = a_in[12]^b_in[12];
assign n85_adder = a_in[12]&b_in[12];
assign n80_adder = a_in[13]^b_in[13];
assign n79_adder = a_in[13]&b_in[13];
assign n78_adder = a_in[14]^b_in[14];
assign n77_adder = a_in[14]&b_in[14];
assign n74_adder = a_in[15]^b_in[15];
assign n73_adder = a_in[15]&b_in[15];
assign n72_adder = a_in[16]^b_in[16];
assign n71_adder = a_in[16]&b_in[16];
assign n70_adder = a_in[17]^b_in[17];
assign n69_adder = a_in[17]&b_in[17];
assign n66_adder = a_in[18]^b_in[18];
assign n65_adder = a_in[18]&b_in[18];
assign n64_adder = a_in[19]^b_in[19];
assign n63_adder = a_in[19]&b_in[19];
assign n58_adder = a_in[20]^b_in[20];
assign n57_adder = a_in[20]&b_in[20];
assign n56_adder = a_in[21]^b_in[21];
assign n55_adder = a_in[21]&b_in[21];
assign n54_adder = a_in[22]^b_in[22];
assign n53_adder = a_in[22]&b_in[22];
assign n42_adder = a_in[23]^b_in[23];
assign n41_adder = a_in[23]&b_in[23];
assign n40_adder = a_in[24]^b_in[24];
assign n39_adder = a_in[24]&b_in[24];
assign n38_adder = a_in[25]^b_in[25];
assign n37_adder = a_in[25]&b_in[25];
assign n32_adder = a_in[26]^b_in[26];
assign n31_adder = a_in[26]&b_in[26];
assign n30_adder = a_in[27]^b_in[27];
assign n29_adder = a_in[27]&b_in[27];
assign n25_adder = a_in[28]^b_in[28];
assign n26_adder = a_in[28]&b_in[28];
assign n24_adder = a_in[29]^b_in[29];
assign n23_adder = a_in[29]&b_in[29];
assign n22_adder = a_in[30]^b_in[30];
assign n21_adder = a_in[30]&b_in[30];
assign n18_adder = a_in[31]^b_in[31];
assign n17_adder = a_in[31]&b_in[31];
assign n13_adder = a_in[32]^b_in[32];
assign n14_adder = ~(a_in[32]^b_in[32]);
assign w34 = n81_adder| n82_adder;
assign n1_adder = n82_adder ? n4_adder : n3_adder;
assign n2_adder = w34 ? n4_adder : n3_adder;
assign w35 = n43_adder| n44_adder;
assign n3_adder = n44_adder ? n6_adder : n5_adder;
assign n4_adder = w35 ? n6_adder : n5_adder;
assign w36 = n33_adder| n34_adder;
assign n5_adder = n34_adder ? n8_adder : n7_adder;
assign n6_adder = w36 ? n8_adder : n7_adder;
assign w37 = n27_adder| n28_adder;
assign n7_adder = n28_adder ? n10_adder : n9_adder;
assign n8_adder = w37 ? n10_adder : n9_adder;
assign w38 = n25_adder| n26_adder;
assign n9_adder = n26_adder ? n12_adder : n11_adder;
assign n10_adder = w38 ? n12_adder : n11_adder;
assign w39 = n15_adder| n16_adder;
assign n11_adder = n16_adder ? n14_adder : n13_adder;
assign n12_adder = w39 ? n14_adder : n13_adder;
assign n15_adder = n18_adder&n20_adder;
assign n16_adder = (n19_adder&n18_adder)|n17_adder;
assign n20_adder = n22_adder&n24_adder;
assign n19_adder = (n23_adder&n22_adder)|n21_adder;
assign n27_adder = n30_adder&n32_adder;
assign n28_adder = (n31_adder&n30_adder)|n29_adder;
assign n33_adder = n36_adder&n42_adder;
assign n34_adder = (n41_adder&n36_adder)|n35_adder;
assign n36_adder = n38_adder&n40_adder;
assign n35_adder = (n39_adder&n38_adder)|n37_adder;
assign n43_adder = n46_adder&n76_adder;
assign n44_adder = (n75_adder&n46_adder)|n45_adder;
assign n46_adder = n48_adder&n74_adder;
assign n45_adder = (n73_adder&n48_adder)|n47_adder;
assign n48_adder = n50_adder&n60_adder;
assign n47_adder = (n59_adder&n50_adder)|n49_adder;
assign n50_adder = n52_adder&n58_adder;
assign n49_adder = (n57_adder&n52_adder)|n51_adder;
assign n52_adder = n54_adder&n56_adder;
assign n51_adder = (n55_adder&n54_adder)|n53_adder;
assign n60_adder = n62_adder&n68_adder;
assign n59_adder = (n67_adder&n62_adder)|n61_adder;
assign n62_adder = n64_adder&n66_adder;
assign n61_adder = (n65_adder&n64_adder)|n63_adder;
assign n68_adder = n70_adder&n72_adder;
assign n67_adder = (n71_adder&n70_adder)|n69_adder;
assign n76_adder = n78_adder&n80_adder;
assign n75_adder = (n79_adder&n78_adder)|n77_adder;
assign n81_adder = n84_adder&n94_adder;
assign n82_adder = (n93_adder&n84_adder)|n83_adder;
assign n84_adder = n86_adder&n88_adder;
assign n83_adder = (n87_adder&n86_adder)|n85_adder;
assign n88_adder = n90_adder&n92_adder;
assign n87_adder = (n91_adder&n90_adder)|n89_adder;
assign n94_adder = n96_adder&n98_adder;
assign n93_adder = (n97_adder&n96_adder)|n95_adder;
assign n98_adder = n100_adder&n102_adder;
assign n97_adder = (n101_adder&n100_adder)|n99_adder;
assign n102_adder = n104_adder&n110_adder;
assign n101_adder = (n109_adder&n104_adder)|n103_adder;
assign n104_adder = n106_adder&n108_adder;
assign n103_adder = (n107_adder&n106_adder)|n105_adder;
assign n0 = n113_adder&n115_adder;
assign n111_adder = (n114_adder&n113_adder)|n112_adder;
assign n115_adder = n117_adder&n127_adder;
assign n114_adder = (n126_adder&n117_adder)|n116_adder;
assign n117_adder = n119_adder&n121_adder;
assign n116_adder = (n120_adder&n119_adder)|n118_adder;
assign n121_adder = n123_adder&n125_adder;
assign n120_adder = (n124_adder&n123_adder)|n122_adder;
endmodule // adder